[latexpage]

这几天我在李俊杰、Mathematica的帮助下推导了极坐标下的二维布朗运动的统计。一开始我就觉得，这是很基本的问题，应该会有相应的例题或课件直接给出答案。但是一开始搜都搜不到。我用体育老师教的数学推了半天，出结果之后，就立马搜到资料了。只当作上天逼我练习一下大学的数学吧。

我要考虑的问题是二维无规行走的极坐标的统计，即极径和极角的分布。之前我总结过了二维和三维无规行走的极径分布分别是Rayleigh分布和Maxwell分布，这都是直角坐标的期望值为零的情况。本文一是要考虑期望值不为零的情况，二是不光考虑极径的分布，还要考虑极角的。

二维无规行走的“轨迹中心”

一个走了N步的二维无规行走轨迹应该是有其中心的。例如，可以定义这个中心为无规行走的x坐标和y坐标的期望值$\mu_X$和$\mu_Y$。这样的定义严格来说并不实用，因为对于给定的有限步数的轨迹，我们无法知道期望值，只能计算均值。后者只有$N\rightarrow\infty$时才是期望值。为了实验方便，我定义二维无规行走的轨迹“中心”是其起始坐标$\left(x_0,y_0\right)$。这样，不仅对任意一个给定的轨迹都能直接说出其“中心”，还能主动实现一个给定中心的“无规行走”——只要从你的行走是从那个中心开始的就行。凭直观想象，一个从点$\left(x_0,y_0\right)$出发的无规行走，只要步数$N$足够大，就有$\mu_X=x_0$和$\mu_Y=y_0$。当然，这是为了实验的思考。接下来的推导都是谈期望值

期望值为零的情况

首先，考虑一个“在原点处”的无规行走，即其x坐标和y坐标的期望值$\mu_X=\mu_Y=0$，方差都是$\sigma^2$（各向同性）。这时其极坐标的极径和极角$r$和$\theta$的分布分别为一个Rayleigh分布和一个均匀分布：

\begin{equation}\label{eq:1}
p_R\left(r\right)=\frac{r}{\sigma^2}\exp\left[-\frac{r^2}{2\sigma^2}\right]
\end{equation}
\begin{equation}\label{eq:2}
p_\Theta\left(\theta\right)=\frac{1}{2\pi}
\end{equation}

期望值不为零的情况

考虑“位于极坐标中点$\left(\mu_r,\mu_\theta\right)$处的无规行走，即其直角坐标x和y的期望值为$\mu_X和\mu_Y$，方差都是$\sigma^2$（各向同性）。于是

\begin{equation}\label{eq:3}
\begin{aligned}
\mu_r&=\sqrt{\mu_X^2+\mu_Y^2}
\\
\mu_\theta&=\left\{\begin{matrix}
\arctan\frac{\mu_Y}{\mu_X}, & x>0\\
\arctan\frac{\mu_Y}{\mu_X}+\pi, &x<0
\end{matrix}\right.
\end{aligned}\end{equation}

则极径$r$和极角$\theta$的联合分布为

\begin{equation}\label{eq:4}
p_{R\Theta}\left(r,\theta\right)=\frac{r}{2\pi\sigma^2}\exp\left[-\frac{r^2+\mu_r^2-2r\mu_r\cos\left(\theta-\mu_\theta\right)}{2\sigma^2}\right]
\end{equation}

由于无规行走的极径和极角是相互独立的随机量，所以求两个边缘分布就可以了。

\begin{equation}
\begin{aligned}
p_R\left(r\right)&=\int_0^{2\pi}p_{R\Theta}d\theta\\
p_\Theta\left(\theta\right)&=\int_0^\infty p_{R\Theta}dr
\end{aligned}
\end{equation}

这两个积分都无法用初等函数表示。我是用Mathematica来算的，结果如下：

\begin{equation}\label{eq:6}
p_R\left(r\right)=\frac{r}{\sigma^2}I_0\left(\frac{r\mu_r}{\sigma^2}\right)\exp\left(-\frac{r^2+\mu_r^2}{2\sigma^2}\right)
\end{equation}

\begin{equation}\label{eq:7}
\begin{aligned}
p_\Theta\left(\theta\right)=&\frac{1}{\sqrt{8\pi\sigma^2}}\mu_r\cos\left(\theta-\mu_\theta\right)\exp\left[-\frac{\mu_r^2\sin^2\left(\theta-\mu_\theta\right)}{2\sigma^2}\right]\times \\
&\left[\mathrm{erf}}\left(\frac{\mu_r\cos\left(\theta-\mu_\theta\right)}{\sqrt{2\sigma^2}}\right)+1\right]+\frac{1}{2\pi}\exp\left(-\frac{\mu_r^2}{2\sigma^2}\right)
\end{aligned}
\end{equation}

其中，$I_0\left(x\right)$是零阶第一类Bessel函数

\begin{equation}
I_0\left(x\right)=\frac{1}{\pi}\int_0^\pi\exp\left(x\cos\theta\right)d\theta
\end{equation}

$\mathrm{erf}\left(x\right)$是误差函数

\begin{equation}
\mathrm{erf}\left(x\right)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt
\end{equation}

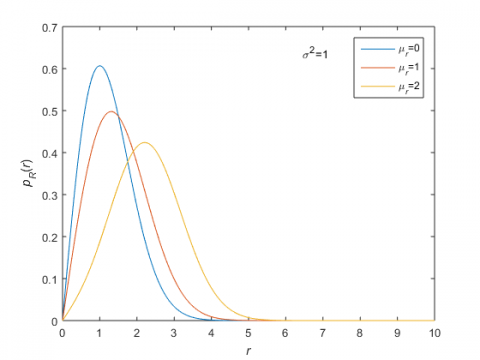
式(\ref{eq:6})其实就是Rice分布，当$\mu_r=0$时退化为Rayleigh分布（式(\ref{eq:1})）。下图是固定$\sigma^2=1$，$\mu_r=0,1,2$的分布曲线：

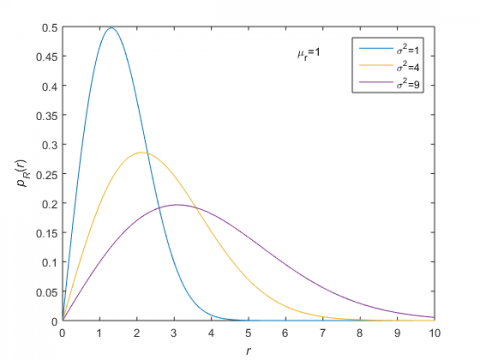
下图是固定$\mu_r=1$，$\sigma^2=1,2,3$的分布曲线：

作为极径的分布，Rice分布与极角的期望$\mu_\theta$无关。而极角的分布（式(\ref{eq:7})）与$\mu_r$和$\mu_\theta$都有关。这个分布是否已有人名，我没有找到。我只找到一篇文章讨论更加一般的情况，即两组高斯量X和Y期望值$\mu_x\neq\mu_y\neq0$，且它们的方差也各不相等$\sigma_x\neq\sigma_y$；而且X坐标和Y坐标还是相关的，它们的协方差系数$\rho\neq0$的情况[1]。我是算出式(\ref{eq:7})之后才找到这篇论文的，唯一安慰就是一对照发现我好歹算对了。

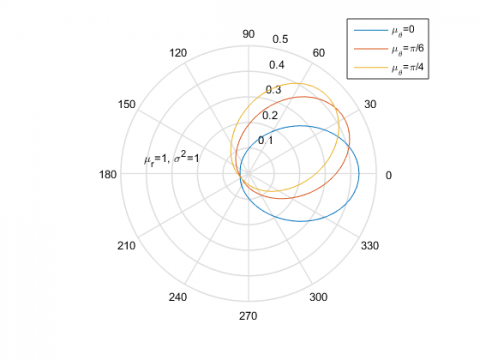
式(\ref{eq:7})在$\mu_r=0$时退化为均一分布$\frac{1}{2\pi}$（式(\ref{eq:2})），这是“在原点处”的无规行走的结果。可以想象，一个远离原点处的二维无规行走，其轨迹相对原点的极角涨落基本会分布在一个很窄的范围之内，而且这个范围主要依赖这个无规行走的“位置”。下图是固定$\mu_r=1$和$\sigma^2=1$，$\mu_\theta=0,\frac{\pi}{6},\frac{\pi}{4}$的结果：

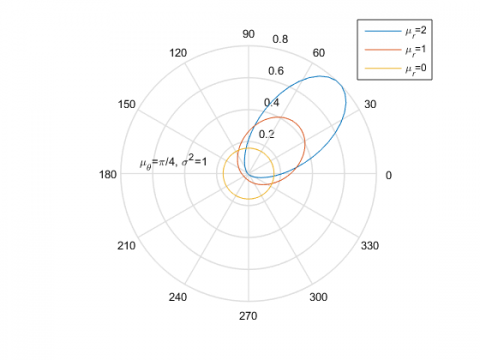
再仔细想，一个给定方差的无规行走，如果离原点近一些，其轨迹的极角涨落会宽一些。下图是固定$\mu_\theta=\frac{\pi}{4}$和$\sigma^2=1$，$\mu_\theta=0,1,2$的结果：

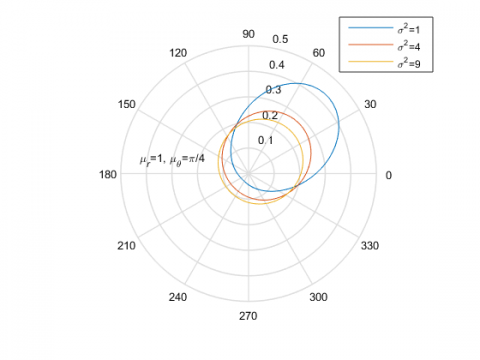
最后，看一下固定$\mu_r=1$和$\mu_\theta=\frac{\pi}{4}$，$\sigma^2=1,4,9$的结果：

References

1. P. Dharmawansa, N. Rajatheva, and C. Tellambura, "Envelope and phase distribution of two correlated gaussian variables", IEEE Transactions on Communications, vol. 57, pp. 915-921, 2009. http://dx.doi.org/10.1109/TCOMM.2009.04.070065